Afgeleide functies — wat betekent dat eigenlijk?
Stel je voor: je bekijkt een auto die rijdt. Je weet de afstand die hij in de tijd aflegt, bijvoorbeeld via een formule. Maar hoe kom je erachter hoe snel de auto op een precies tijdstip rijdt?
Het gemiddelde over een paar seconden kun je berekenen, maar dat zegt niets over het exacte moment. Om dat idee te begrijpen gebruiken we de afgeleide functie.
Vraag 1
Een auto legt een afstand af volgens de formule
![]()
waarbij ![]() in meters en
in meters en ![]() in seconden is. Hoe snel rijdt de auto op precies
in seconden is. Hoe snel rijdt de auto op precies ![]() seconden?
seconden?
Uitwerking:
- We berekenen eerst de gemiddelde snelheid op een klein interval. De gemiddelde snelheid tussen
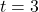 en
en 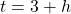 is gegeven door:
is gegeven door:
![Rendered by QuickLaTeX.com \[v_{\text{gem}}(h) = \frac{s(3+h)-s(3)}{h}.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-ba601eb2b88a92a478694d215a7d2b79_l3.png)
- Als we dan de formule invullen krijgen we:
![Rendered by QuickLaTeX.com \[s(3+h)=5(3+h)^2=45+30h+5h^2.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-84fa768d2246e08491a1ba56afec0210_l3.png)
![Rendered by QuickLaTeX.com \[v_{\text{gem}}(h)=\frac{(45+30h+5h^2)-45}{h}=30+5h.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-dd4baa5e5b195cdcda2511ea3f2440a4_l3.png)
- Voor steeds kleinere
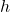 nadert de snelheid
nadert de snelheid 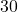 . Dus
. Dus
![Rendered by QuickLaTeX.com \[v(3)=\lim_{h\to 0}(30+5h)=30.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-0ab32c4651df6b15dcd0588090f4e1e6_l3.png)
Conclusie: Op ![]() seconden rijdt de auto 30 m/s. Dit is precies wat we bedoelen met de afgeleide: de snelheid op één moment.
seconden rijdt de auto 30 m/s. Dit is precies wat we bedoelen met de afgeleide: de snelheid op één moment.
Vraag 2
Een fietser legt afstand af volgens ![]() . Hoe verschilt de snelheid van deze fietser van de auto uit vraag 1?
. Hoe verschilt de snelheid van deze fietser van de auto uit vraag 1?
Uitwerking:
- Gemiddelde snelheid tussen
 en
en  :
:
![Rendered by QuickLaTeX.com \[\frac{f(t+h)-f(t)}{h}=\frac{4(t+h)-4t}{h}=\frac{4h}{h}=4.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-62196622aefb122f03fbb61fd4f9fc74_l3.png)
- Er valt niets meer te benaderen: de snelheid is altijd precies 4.
Conclusie: Bij een rechte lijn is de snelheid overal hetzelfde: de afgeleide is constant. Bij een kromme (zoals ![]() ) verandert de snelheid en is de afgeleide afhankelijk van
) verandert de snelheid en is de afgeleide afhankelijk van ![]() .
.
Vraag 3
Een wandelaar loopt langs een rechte weg en keert plotseling om. De positie wordt beschreven door
![]()
Wat is de snelheid precies op ![]() ?
?
Uitwerking:
- Voor
 : gemiddelde verandering
: gemiddelde verandering 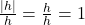 .
. - Voor
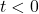 : gemiddelde verandering
: gemiddelde verandering 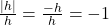 .
. - De linker- en rechterkant geven dus verschillende uitkomsten.
Conclusie: Er bestaat geen duidelijke snelheid op ![]() . Bij een knik of plotselinge richtingsverandering bestaat de afgeleide niet.
. Bij een knik of plotselinge richtingsverandering bestaat de afgeleide niet.
Samenvatting
- De afgeleide is de instantane snelheid van verandering.
- Bij een kromme functie (zoals een parabool) verandert de afgeleide met
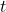 .
. - Bij een rechte lijn is de afgeleide constant.
- Bij een knik bestaat de afgeleide niet.