Technieken voor differentiëren
Nu je weet wat een afgeleide betekent, gaan we kijken naar de regels die je helpen om functies stap voor stap af te leiden. Elke regel vertelt je wat er gebeurt als je een bepaald type bewerking ziet in een functie: een som, een product, een breuk of een samenstelling van functies.
Belangrijkste regels
- Somregel: Als je twee functies optelt, dan is de afgeleide gewoon de som van de afzonderlijke afgeleiden:
![Rendered by QuickLaTeX.com \[(f(x)+g(x))' = f'(x)+g'(x).\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-b3b5cf8d8cf1c78a77c189da59cfcbdc_l3.png)
- Productregel: Bij een vermenigvuldiging geldt
![Rendered by QuickLaTeX.com \[(f(x)\cdot g(x))' = f'(x)\cdot g(x)+f(x)\cdot g'(x).\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-c6fd02a3c3956ef687ea0fcd8a7d8bf0_l3.png)
- Quotiëntregel: Bij een deling geldt
![Rendered by QuickLaTeX.com \[\left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x)\cdot g(x) - f(x)\cdot g'(x)}{(g(x))^2}.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-a66b69d7490598407cd795320457de60_l3.png)
- Kettingregel: Als
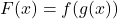 , dus een functie in een functie, dan geldt
, dus een functie in een functie, dan geldt
![Rendered by QuickLaTeX.com \[F'(x)=f'(g(x))\cdot g'(x).\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-a6846259e88131938da4585524df67f2_l3.png)
Vraag 1 — Productregel
Bepaal de afgeleide van
![]()
Uitwerking:
Deze functie bestaat uit een product: het ene stuk is ![]() , het andere stuk is
, het andere stuk is ![]() .
.
- Afgeleiden van de losse stukken:
![Rendered by QuickLaTeX.com \[(x^2)'=2x, \quad (\sin(x))'=\cos(x).\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-bd1572ae29a78c2c5192ff8a584eb2c7_l3.png)
- Pas de productregel toe: “Eerst het eerste afgeleiden en het tweede laten staan, plus het eerste laten staan en het tweede afgeleiden.”
![Rendered by QuickLaTeX.com \[h'(x)=2x\cdot \sin(x) + x^2\cdot \cos(x).\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-88f000cc95b1ec7ecaeda29d8baf6e21_l3.png)
Conclusie: Bij een product komt er altijd twee termen uit: één keer met de afgeleide van de eerste factor, en één keer met de afgeleide van de tweede.
Vraag 2 — Quotiëntregel
Bepaal de afgeleide van
![]()
Uitwerking:
Dit is een breuk, dus we gebruiken de quotiëntregel.
- Hier is de teller
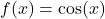 en de noemer
en de noemer 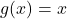 .
. - Afgeleiden van de losse stukken:
![Rendered by QuickLaTeX.com \[f'(x)=-\sin(x), \quad g'(x)=1.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-7781ea563efda75eb2daf75bf4052ef6_l3.png)
- Quotiëntregel zegt: “Teller is de afgeleide van de bovenkant keer de onderkant, min de bovenkant keer de afgeleide van de onderkant, gedeeld door de onderkant in het kwadraat.”
![Rendered by QuickLaTeX.com \[k'(x)=\frac{(-\sin(x))\cdot x - \cos(x)\cdot 1}{x^2}.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-7db96bcaddabd045b06f4562e7c2d18e_l3.png)
- Dus:
![Rendered by QuickLaTeX.com \[k'(x)=\frac{-x\sin(x)-\cos(x)}{x^2}.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-42e4fc134dc6db7636158aeb442c6f24_l3.png)
Conclusie: Bij een breuk moet je goed de volgorde onthouden: eerst afgeleide boven × onder, daarna min boven × afgeleide onder, en dat alles over de noemer in het kwadraat.
Vraag 3 — Kettingregel
Bepaal de afgeleide van
![]()
Uitwerking:
Hier zit een functie in een functie: buiten zit een ![]() , binnen zit
, binnen zit ![]() .
.
- Buitenkant:
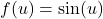 met afgeleide
met afgeleide 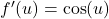 .
. - Binnenkant:
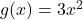 met afgeleide
met afgeleide 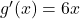 .
. - Kettingregel: vermenigvuldig de afgeleide van de buitenkant met de afgeleide van de binnenkant:
![Rendered by QuickLaTeX.com \[m'(x)=\cos(3x^2)\cdot 6x.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-72e183732bc5878d7e34e83839febfd8_l3.png)
Conclusie: Bij een samenstelling van functies doe je altijd eerst de buitenste afgeleide, en vermenigvuldig je die met de afgeleide van wat er binnen staat.
Vraag 4 — Alles samen
Bepaal de afgeleide van
![]()
Uitwerking:
Hier komen alle regels bij elkaar:
- In de teller zie je een som (
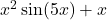 ),
), - daarin ook een product (
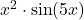 ),
), - en in die sinus ook nog een ketting (
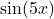 ).
). - Tot slot staat het geheel in een breuk, dus de quotiëntregel moet worden gebruikt.
- Noemer:
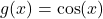 , met afgeleide
, met afgeleide 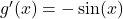 .
. - Teller:
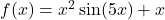 .
.
- Dit is een som, dus leid de twee termen apart af.
- Eerste term:
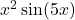 . Dit is een product:
. Dit is een product:
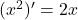 ,
, 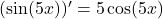 .
.
Dus:![Rendered by QuickLaTeX.com \[(x^2\sin(5x))' = 2x\sin(5x)+5x^2\cos(5x).\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-1de386c965bfb31f03dcbe3ae13865fe_l3.png)
- Tweede term:
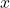 . Afgeleide is gewoon 1.
. Afgeleide is gewoon 1. - Samen:
![Rendered by QuickLaTeX.com \[f'(x)=2x\sin(5x)+5x^2\cos(5x)+1.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-dd1011632fcf057beb5dc978e7c0760d_l3.png)
- Quotiëntregel:
![Rendered by QuickLaTeX.com \[p'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{(g(x))^2}.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-df69760b966b292bb6e50f36b63da73c_l3.png)
- Invullen:
![Rendered by QuickLaTeX.com \[p'(x)=\frac{[2x\sin(5x)+5x^2\cos(5x)+1]\cos(x)-[x^2\sin(5x)+x]\cdot(-\sin(x))}{\cos^2(x)}.\]](https://bijlesbeta.nl/wp-content/ql-cache/quicklatex.com-9c63fd06925451d836534a85005e31e1_l3.png)
Conclusie: Soms moet je meerdere regels achter elkaar toepassen. Het helpt om de functie in stukjes te analyseren: zie je een som, een product, een ketting, of een quotiënt? Vaak zijn ze gecombineerd, en dan pas je de regels in de juiste volgorde toe.